


Next: Stage 5
Up: Stage 4
Previous: How we Found the
There are two major obstacles when deciphering a Vigenère
cipher. The first is to find the length of the keyword
superposed on the plaintext, and the second is to find
the shift between adjacent letters in the keyword.
If the keyword length is five, every fifth letter in the ciphertext
have been shifted the same distance. This means that for the offsets
0, 1, 2, 3, 4, the text obtained by reading every fifth word will be
an ordinary Caesar shift of the plaintext. Given a string
x of n characters, the index of coincidence of
x, denoted
Ic(x) is defined as the probability
that two random elements of
x are identical. If the
frequencies of the 26 letters in
x are denoted
f0,..., f25, this probability can be written
Ic(x) = 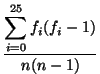 . . |
(1) |
For a completely random string this value will be approximately
1/26 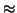 0.038. However, if we let pi be the probability that a
random letter in English text is i, then for an English text
x,
0.038. However, if we let pi be the probability that a
random letter in English text is i, then for an English text
x,
If the different letters in a text are shifted
with different shifts this text will look like random text. However,
if they are shifted with the same shift the index of coincidence
should be that of the plaintext. If we compute the mean of the index
of coincidence for the text obtained by reading every fifth letter for
the five offsets we thus expect that the index of coincidence will
be closer to 0.065 than to 0.038 if five is the correct keyword
length. This is also what we observe above.
The next problem is to determine the difference in shifts between the
adjacent letters in the text. This is done in a similar way. Let
x and
y be two strings with nx and nyletters, respectively. The mutual index of coincidence of
xand
y, denoted
MIc(x,y), is defined
as the probability that a random element of
x is identical
to a random element of
y. If
fx0,..., fx25 and
fy0,..., fy25 is the frequencies of the 26 letters in
x and
y, respectively, this probability can be
written
MIc(x,y) = 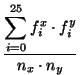 . . |
(3) |
Assume once more that the keyword length is five. Let
y1,...,y5 be the five substrings obtained by
reading every fifth letter for the five different offsets. The
substrings
yi are all obtained by a shift encryption of the
plaintext. Assume that
K = (k1,..., k5) is the keyword. It is
quite easy to see that in this case
MIc(yi,yj) 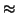
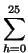 ph - ki, ph - kj = ph - ki, ph - kj = 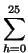 ph, ph + ki - kj ph, ph + ki - kj |
(4) |
where the subscripts are reduced modulo 26. If we test all possible
relative shifts of two strings of English text we will see that when
the relative shift is 0, the mutual coincidence will be approximately
0.065; and otherwise it lies between 0.030 and 0.045. This means that if
we test all possible values for ki - kj for the two substrings
yi and
yj, the mutual coincidence should be
close to 0.065 for the correct relative shift and between 0.030and 0.045 in the other cases. This will give us an linear system
of equations for the five shifts
k1,..., k5 which can be solved
and which will yield the relative shifts for the five substrings.
Now we only have 26 possible keywords and plaintexts, and a visual
inspection easily reveals the solution.



Next: Stage 5
Up: Stage 4
Previous: How we Found the
solvers@codebook.org
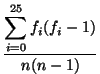 .
.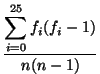 .
.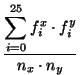 .
.